前言
"color: #ff0000">1. BF算法
"application/x-tex">Bruce-ForceBruce"application/x-tex">S=ABACABABS=ABACABAB,模式串
def BF(substrS, substrT):
if len(substrT) > len(substrS):
return -1
j = 0
t = 0
while j < len(substrS) and t < len(substrT):
if substrT[t] == substrS[j]:
j += 1
t += 1
else:
j = j - t + 1
t = 0
if t == len(substrT):
return j - t
else:
return -1
2. KMP算法
"normal">.
"normal">"
"false">(
"normal">′
"text-align: center"> "text-align: left">"text-align: center">
"text-align: left">"text-align: center">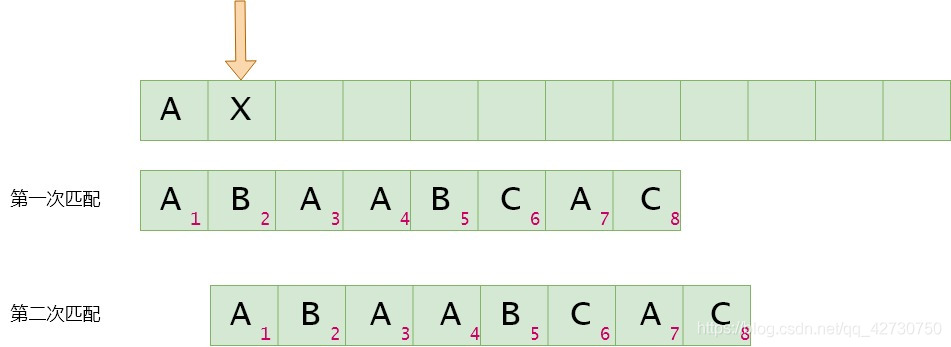 "text-align: left">"normal">"
"text-align: left">"normal">"
"normal">"
 "text-align: left">"normal">"
"text-align: left">"normal">"
"normal">"
"normal">"
"normal">"
 "text-align: left">如果模式串8号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为
"text-align: left">如果模式串8号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为
"text-align: left">
位编号
1
2
3
4
5
6
7
8
索引
0
1
2
3
4
5
6
7
模式串
A
B
A
A
B
C
A
C
next
-1
0
0
1
1
2
0
1
"text-align: center"> "text-align: left">"application/x-tex">T_j=T_tTj"false">[
"text-align: left">"application/x-tex">T_j=T_tTj"false">[
"normal">≠
"htmlcode">
def getNext(substrT):
next_list = [-1 for i in range(len(substrT))]
j = 0
t = -1
while j < len(substrT) - 1:
if t == -1 or substrT[j] == substrT[t]:
j += 1
t += 1
# Tj=Tt, 则可以到的next[j+1]=t+1
next_list[j] = t
else:
# Tj!=Tt, 模式串T索引为t的字符与当前位进行匹配
t = next_list[t]
return next_list
def KMP(substrS, substrT, next_list):
count = 0
j = 0
t = 0
while j < len(substrS) and t < len(substrT):
if substrS[j] == substrT[t] or t == -1:
# t == -1目的就是第一位匹配失败时
# 主串位置加1, 匹配串回到第一个位置(索引为0)
# 匹配成功, 主串和模式串指针都后移一位
j += 1
t += 1
else:
# 匹配失败, 模式串索引为t的字符与当前位进行比较
count += 1
t = next_list[t]
if t == len(substrT):
# 这里返回的是索引
return j - t, count+1
else:
return -1, count+1
3. KMP算法优化版
"application/x-tex">S=AAABAAAABS=AAABAAAAB,模式串

"text-align: left">"application/x-tex">SS的4号位为模式串
"false">[
def getNextval(substrT):
nextval_list = [-1 for i in range(len(substrT))]
j = 0
t = -1
while j < len(substrT) - 1:
if t == -1 or substrT[j] == substrT[t]:
j += 1
t += 1
if substrT[j] != substrT[t]:
# Tj=Tt, 但T(j+1)!=T(t+1), 这个就和next数组计算时是一样的
# 可以得到nextval[j+1]=t+1
nextval_list[j] = t
else:
# Tj=Tt, 且T(j+1)==T(t+1), 这个就是next数组需要更新的
# nextval[j+1]=上一次的nextval_list[t]
nextval_list[j] = nextval_list[t]
else:
# 匹配失败, 模式串索引为t的字符与当前位进行比较
t = nextval_list[t]
return nextval_list
"htmlcode">
if __name__ == '__main__':
S1 = 'ABACABAB'
T1 = 'ABAB'
S2 = 'AAABAAAAB'
T2 = 'AAAAB'
print('*' * 50)
print('主串S={0}与模式串T={1}进行匹配'.format(S1, T1))
print('{:*^25}'.format('KMP'))
next_list1 = getNext(T1)
print('next数组为: {}'.format(next_list1))
index1_1, count1_1 = KMP(S1, T1, next_list1)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index1_1, count1_1))
print('{:*^25}'.format('KMP优化版'))
nextval_list1 = getNextval(T1)
print('nextval数组为: {}'.format(nextval_list1))
index1_2, count1_2 = KMP(S1, T1, nextval_list1)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index1_2, count1_2))
print('')
print('*' * 50)
print('主串S={0}与模式串T={1}进行匹配'.format(S2, T2))
print('{:*^25}'.format('KMP'))
next_list2 = getNext(T2)
print('next数组为: {}'.format(next_list2))
index2_1, count2_1 = KMP(S2, T2, next_list2)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index2_1, count2_1))
print('{:*^25}'.format('KMP优化版'))
nextval_list2 = getNextval(T2)
print('nextval数组为: {}'.format(nextval_list2))
index2_2, count2_2 = KMP(S2, T2, nextval_list2)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index2_2, count2_2))
"application/x-tex">S=ABACABABS=ABACABAB与模式串
结束语
在写本篇博客之前也是反复看参考书、视频,边画图边去理解它,这篇博客也是反复修改了好几次,最终算是把KMP解决掉了,有关字符串知识的复习也算是基本结束,下面就是刷题了(虽然在LeetCode做过了几道题)。
免责声明:本站资源来自互联网收集,仅供用于学习和交流,请遵循相关法律法规,本站一切资源不代表本站立场,如有侵权、后门、不妥请联系本站删除!
稳了!魔兽国服回归的3条重磅消息!官宣时间再确认!
昨天有一位朋友在大神群里分享,自己亚服账号被封号之后居然弹出了国服的封号信息对话框。
这里面让他访问的是一个国服的战网网址,com.cn和后面的zh都非常明白地表明这就是国服战网。
而他在复制这个网址并且进行登录之后,确实是网易的网址,也就是我们熟悉的停服之后国服发布的暴雪游戏产品运营到期开放退款的说明。这是一件比较奇怪的事情,因为以前都没有出现这样的情况,现在突然提示跳转到国服战网的网址,是不是说明了简体中文客户端已经开始进行更新了呢?
更新日志
- 小骆驼-《草原狼2(蓝光CD)》[原抓WAV+CUE]
- 群星《欢迎来到我身边 电影原声专辑》[320K/MP3][105.02MB]
- 群星《欢迎来到我身边 电影原声专辑》[FLAC/分轨][480.9MB]
- 雷婷《梦里蓝天HQⅡ》 2023头版限量编号低速原抓[WAV+CUE][463M]
- 群星《2024好听新歌42》AI调整音效【WAV分轨】
- 王思雨-《思念陪着鸿雁飞》WAV
- 王思雨《喜马拉雅HQ》头版限量编号[WAV+CUE]
- 李健《无时无刻》[WAV+CUE][590M]
- 陈奕迅《酝酿》[WAV分轨][502M]
- 卓依婷《化蝶》2CD[WAV+CUE][1.1G]
- 群星《吉他王(黑胶CD)》[WAV+CUE]
- 齐秦《穿乐(穿越)》[WAV+CUE]
- 发烧珍品《数位CD音响测试-动向效果(九)》【WAV+CUE】
- 邝美云《邝美云精装歌集》[DSF][1.6G]
- 吕方《爱一回伤一回》[WAV+CUE][454M]







